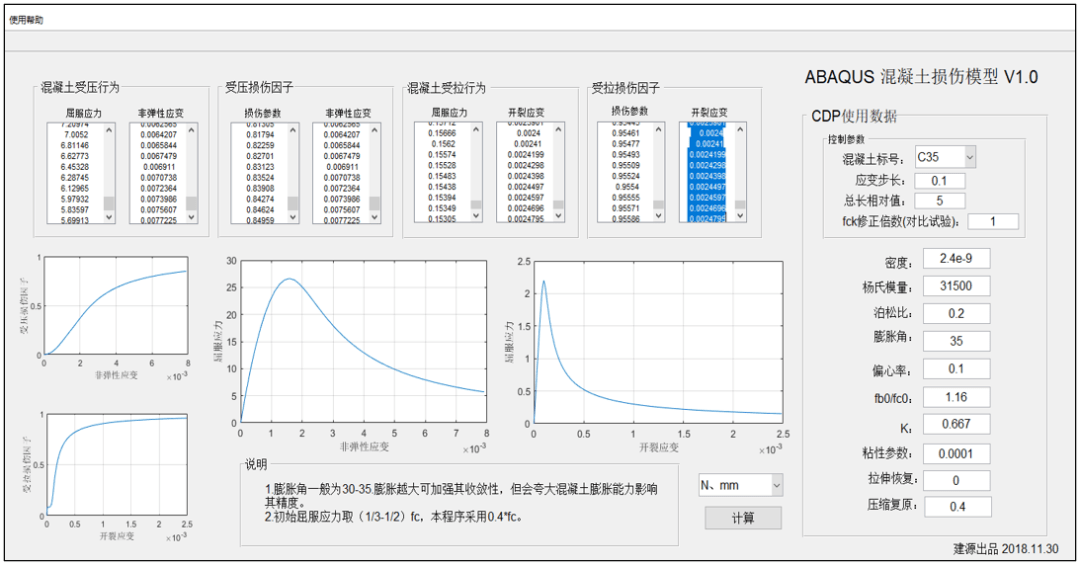
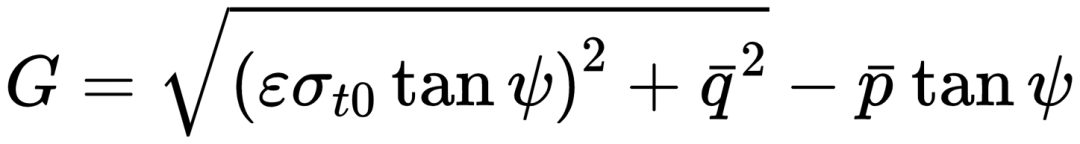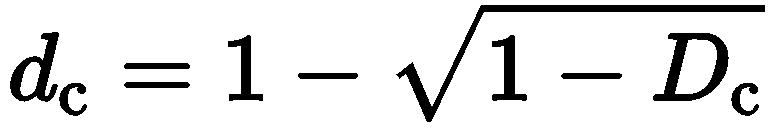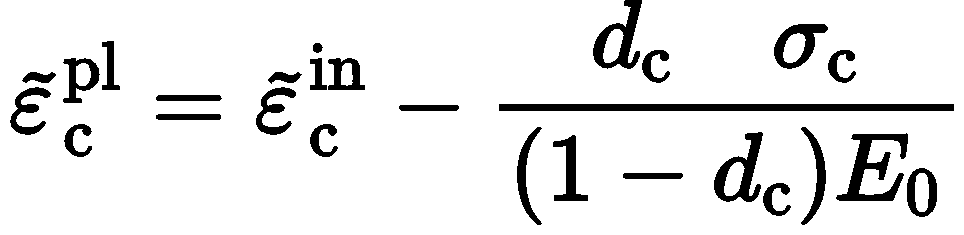1.什么是弹塑性损伤模型
为了了解什么是弹塑性损伤模型,我们需要先了解下,什么是弹塑性模型、弹性损伤模型,再了解弹塑性损伤模型。
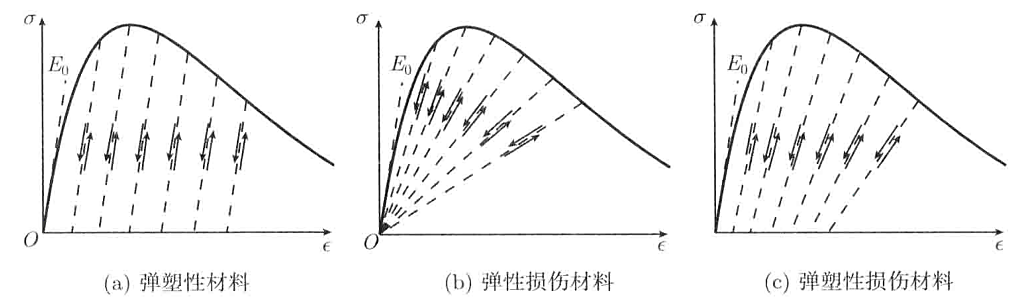
对于弹塑性模型,材料受力超过弹性极限或屈服强度时,应力和应变呈非线性关系,产生不可逆的塑性变形,卸载刚度按初始刚度决定,卸载后出现残余应变的现象。外载进入弹塑性区域,物体产生的变形称弹塑性变形,由弹性变形和塑性变形组成。
弹性损伤模型只考虑损伤对刚度退化的影响,不计不可恢复变形。卸载路径按照原点返回,实质上损伤被考虑成通过割线模量定义的材料刚度退化。材料没有损伤产生或者保持初始损伤值不发展,超过峰值应力后损伤开始发展。弹性损伤模型是基于弹性卸载考虑的,因此高估了材料刚度的退化程度,但可避开捕捉非弹性变形而直接反映材料的软化行为。
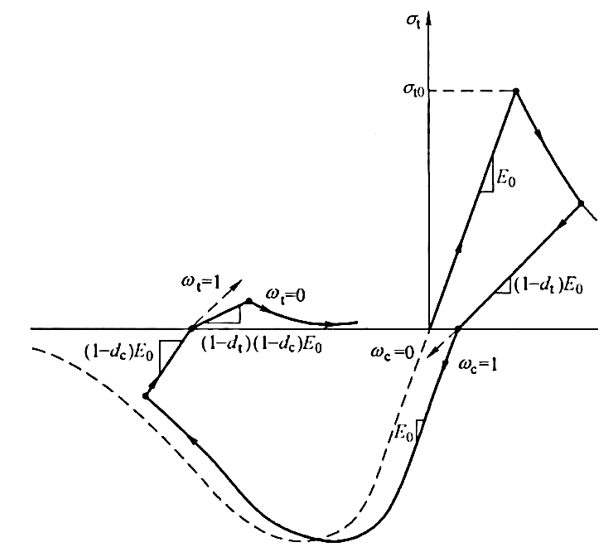
而事实上混凝土卸载时不但表现出刚度退化现象,还存在不可恢复变形,因此采用如下图所示的弹塑性损伤模型更能描述混凝土损伤全过程。
在弹塑性模型中损伤概念的引入,在一定程度上打破了连续介质力学上的连续性假定。因为是以一种特殊的方式(去除损伤、利用应变等效)在连续介质空间中应用经典连续介质力学。
由于混凝土的损伤破坏过程本身就是一种消耗能量的过程,即自由能不断减少的过程。对于混凝土弹塑性损伤模型,通常采用热力学方法建立了塑性损伤和连续损伤模型。由于本构关系是由热力学势函数导出的,因此在热力学环境中是一致的。在热力学方法中,由于需要定义明确的势函数以及状态变量与它们的共轭力之间的结合性,很难根据物理观测构造本构系统,因此这更适合于模拟准脆性材料的混凝土。
将系统的热力学变化过程看成是一种平衡被打破、重建的过程。换句话说,当系统有损伤产生时,当前的平衡状态将被打破,能量耗散趋于稳定时,系统又建立了新的平衡状态。这个热力学过程应符合最小耗能原理或者极值原理。因此最小耗能原理更适用于损伤准则的建立。当已知耗能系统的能量耗散率及其这一过程所必须满足的约束条件,则可以找到满足系统耗能取驻值的条件,由此可建立统一形式的损伤准则。这个损伤准则是混凝土内部产生损伤所必须满足的约束条件,表征了系统损伤过程中能量累积的程度。
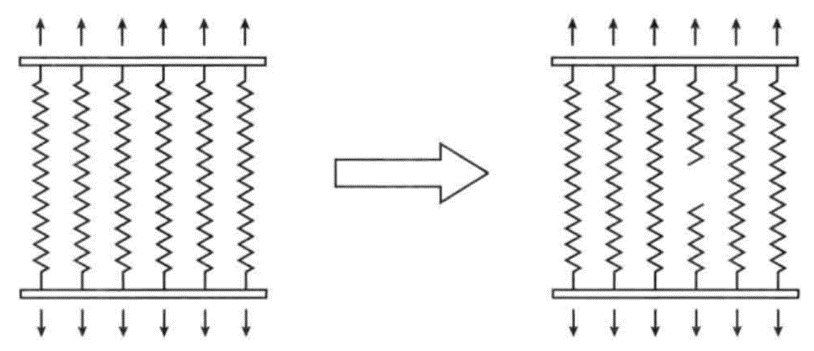
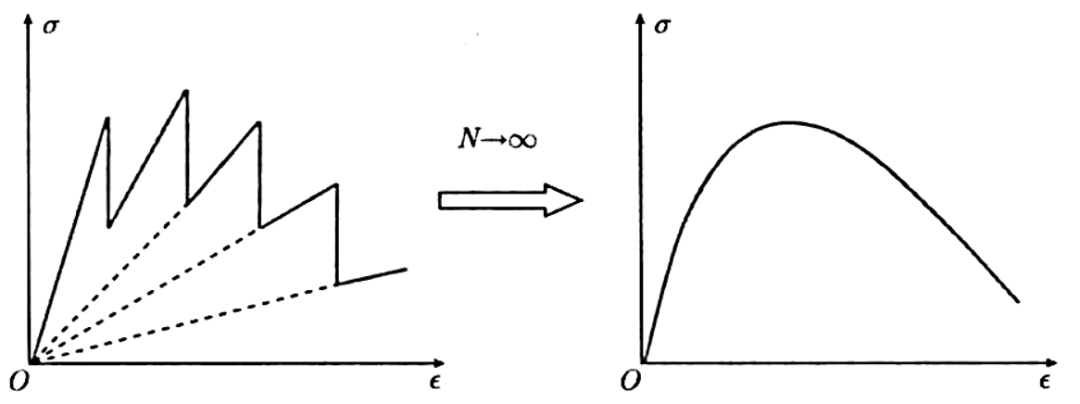
为了更清晰表达混凝土损伤模型示意,可从上图看,在外力小于某一值时,微弹簧系统不发生断裂,相应的应力-应变关系具有线性变化特征。当外部拉力增加,使得具有最小断裂应变的微弹簧的应变达到其断裂界限值时,该微弹簧断裂,其释放的应力由其他微弹簧承担(应力重分布),与此同时,系统整体刚度降低,导致微弹簧系统的应力-应变关系进入非线性变化阶段。随着外部拉力的增加,微弹簧断裂的数量不断增加,应力-应变曲线的非线性愈加显著,表现为应力的增加速率明显小于应变的增加速率。
当在一个增量步内,未损伤部分的应力增加量小于因损伤导致的应力降低量时,即微弹簧断裂造成的平均应力降低大于因外力增加导致的平均应力增长时,应力一应变关系进入下降段。应力一应变上升段与下降段的交点,即为微弹簧系统所代表的细观单元的受拉极限强度。由于各个微弹簧的断裂应变具有随机分布特征,无论是初始损伤的发生时刻,还是后续的应力重分布过程,都将具有典型的随机性特征。因此这不仅解释了损伤导致非线性的物理本质,也同时描述了受拉损伤的随机演化进程。
2.为什么选择砼损伤模型
通过混凝土宏观唯象理论的非线性行为的分析,目前用于描述混凝土力学行为的主要有断裂力学模型和损伤力学模型两种力学模型。
损伤力学模型和断裂力学模型都关心带有缺陷的结构体的性质,借此来评价结构的寿命和安全性。但是损伤力学模型是将缺陷平均处理成连续分布在结构内部,本构关系中包含了微裂缝效应,反映在损伤内变量的变化上。实际结构中不可能只有一条或者几条裂缝,因此,只限于研究局部裂缝的开裂情况从分析的精度上看并非十分可靠。
而断裂力学模型考虑一个事先已形成的宏观裂缝尖端的应力场的奇异性,从而根据断裂能等准则来判裂缝的发展情况。断裂力学模型中裂缝的性质是不包含在本构关系中,而是作为边界条件被考虑。对于宏观裂缝增长的物理认识,断裂力学模型认为是裂缝尖端的应力、应变或者断裂能超过临界值所致,而损伤力学模型也认为是应变或者能量释放率等内变量的累积程度超过损伤门槛值而破坏。
由于结构的破坏往往是开始于损伤的形成和扩展,对混凝土材料而言,带损伤的本构模型是有效的,它不仅可以模拟其非线性行为,包括如刚度退化等性质,还能在宏观上考虑微缺陷和微空洞的平均分布情况,兼顾了一定的细观机制的考虑。即使开裂是随机产生在很小的尺度层次上,但是多条不确定性的微裂缝最终还是汇聚成几条确定性宏观裂缝,损伤理论能够描述多重微开裂发展至单一宏观开裂的全过程,因此该模型对于混凝土构件往复滞回,或者荷载作用下混凝土结构的开裂损伤等具有非线性、随机性的分析具有较好的描述意义。
3.混凝土的动力本构讨论
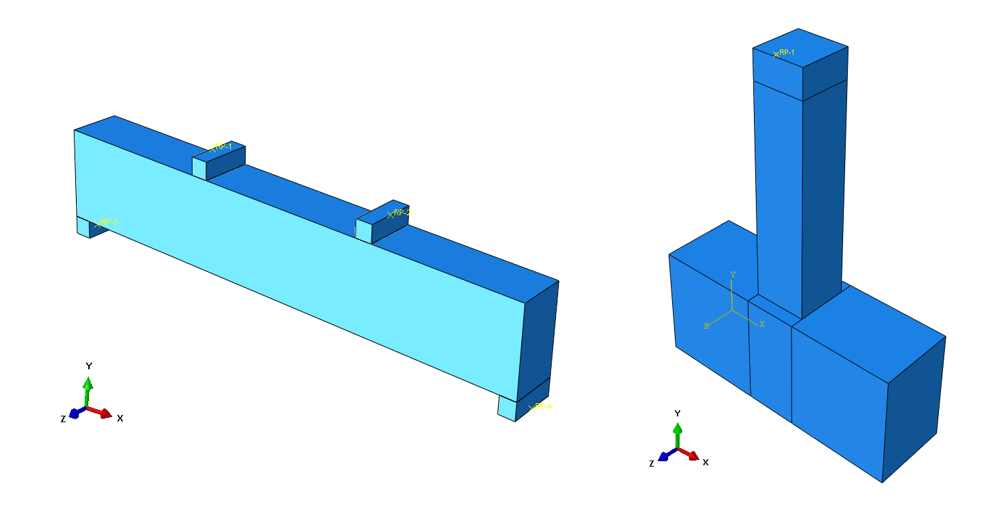
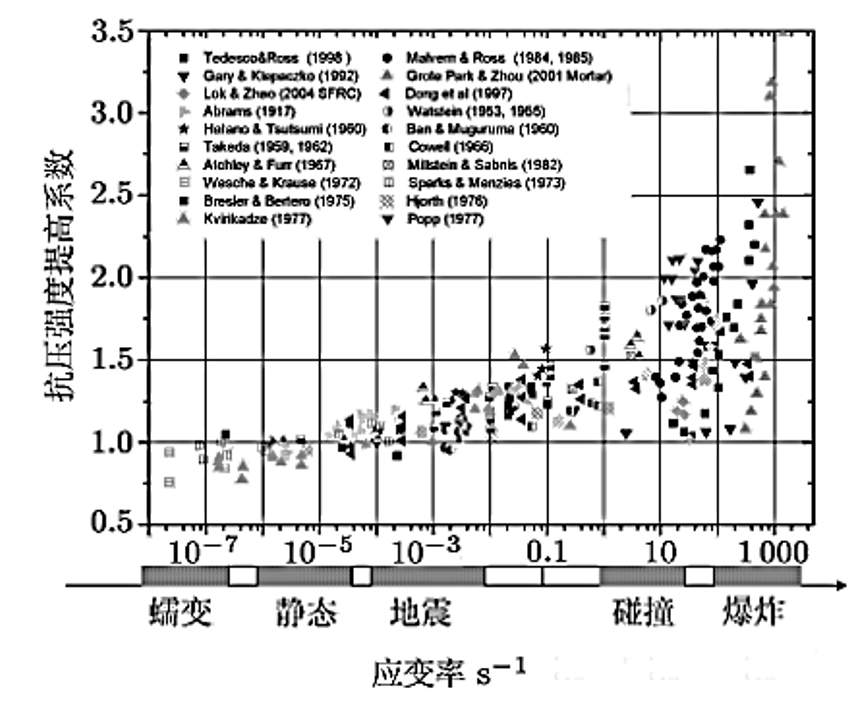
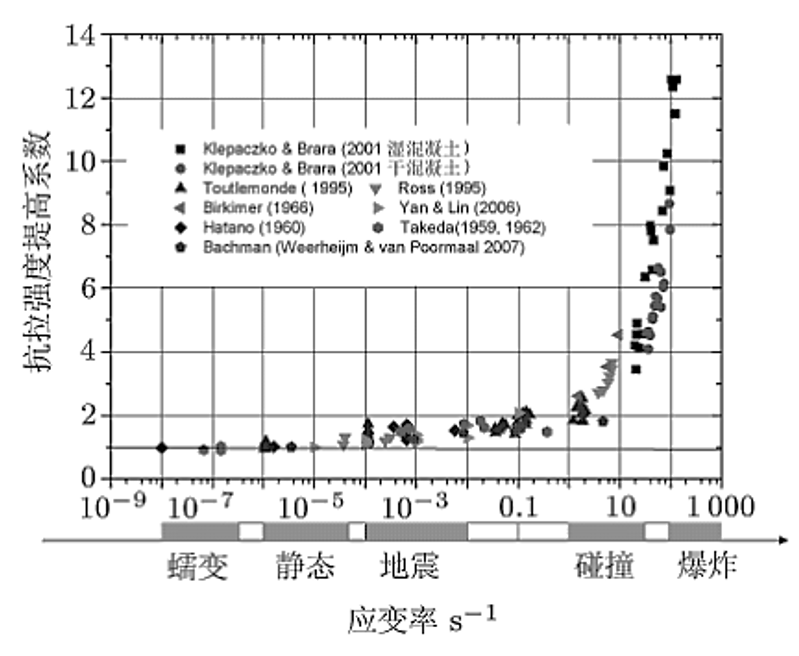
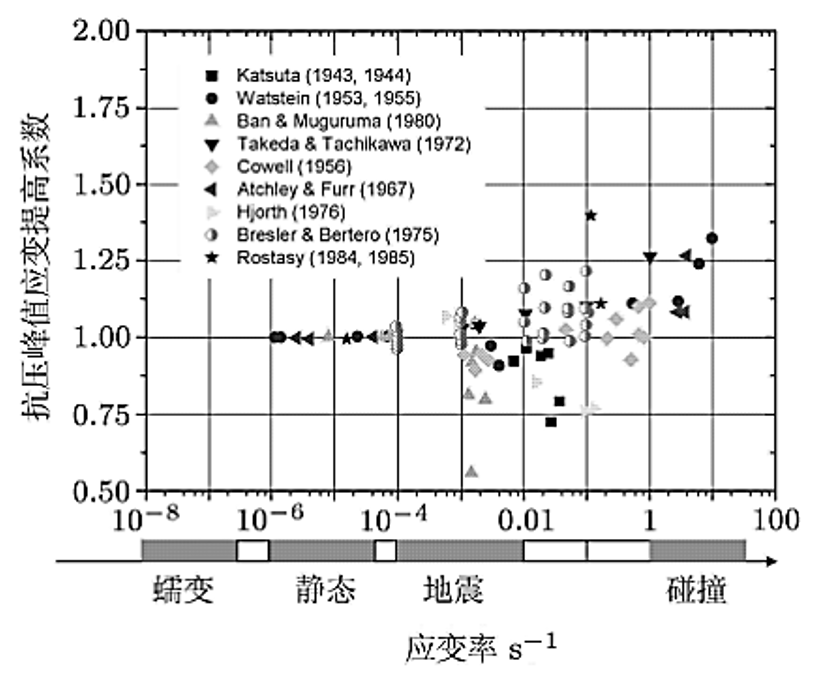
我们会经常基于混凝土损伤模型,应用准静态本构(或者动力本构)对构件进行拟静力往复模拟(如柱子),单调加载模拟(如梁),甚至是碰撞或者冲击模拟。和一切物理科学研究的基本发展过程相类似,为探究宏观常见的灾害(如地震)对混凝土构件动力本构的影响问题将从实验开始展开的。载荷速率对混凝土抗压强度影响的研究成果,在大多数情况下,混凝土动力强度的增长都可以用载荷速率(或应力速率、应变速率)比的对数关系来加以表示。
从下图可以知道,地震在应用准静态本构,进行地震动力模拟,或利用拟静力滞回试验的结果应用到地震工程分析具有一定的可靠性。而碰撞与冲击为了仿真符合实际,应考虑碰撞与冲击混凝土本构。
4.Abq中CDP参数讨论
Abaqus中的CDP模型对于混凝土是连续的、基于塑性的损伤模型。假设两个主要的失效机理是混凝土材料的拉伸开裂和压缩压碎。
模型假设混凝土的单轴拉伸和压缩响应是通过损伤塑性来表征的,在单轴拉伸情况下,应力-应变响应遵循线弹性关系,直到达到失效。失效应力对应于混凝土材料中微观裂纹的发生。超出失效应力后,微观开裂的公式采用软化应力-应变响应来宏观地表示,这样在混凝土结构中产生应变局部化。这样表示虽然进行了简化,但抓住了混凝土响应的主要特征。
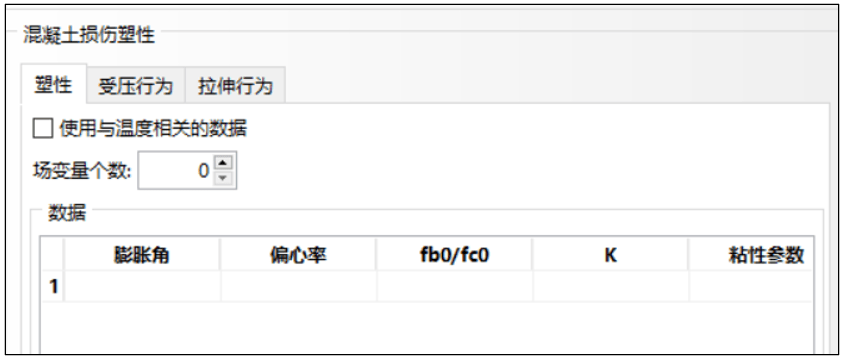
【塑性定义】
对于输入参数,需要我们了解的参数:膨胀角、偏心率、fb0/fc0、K、粘性参数。
(1)膨胀角和偏心率
在Abaqus的CDP中,描述混凝土损伤塑性模型假设非相关的势塑性流动,所用的流动势G是德鲁克-普拉格(Drucker-Prager)静水方程(德鲁克-普拉格强度准则的建立是为了反映岩石的破坏机理):
ψ是在高围压下,平面p-q中所测得到的膨胀角;
δt0是失效时的单轴拉伸应力;
ε是偏心率,可见当偏心率趋近于零时,流动势趋于一条直线。
建议取 流动势偏心率 ε=0.1,这意味着在范围广泛的围压应力值下,材料具有几乎一样的膨胀角。增加偏心率的值,为流动势提供更多的曲率,意味着随着围压的降低,膨胀角的增加更加迅速。如果材料用于低围压应力,则显著小于默认值的偏心率可能导致收敛问题。
建议取 膨胀角 ψ=30~35,当膨胀角越大,表征到构件上的承载力,随着角度取值的增大,框架的极限承载力有一定程度的提高,但提高幅度不是很大。膨胀角如何精确取值到目前为止未有定论,需要依据具体情况而定,一般认为取30°~35°较为合理。
(2)fb0/fc0和K
模型假设混凝土的单轴拉伸和压缩响应是通过损伤塑性来表征的,如何从单轴参数扩展到双轴,CDP模型用fb0/fc0和K参数进行描述。通过试验的双轴受力特征可知:在双向受拉应力状态,二轴抗拉强度与单轴抗拉强度相比无明显变化。当处于一向受压一向受拉时,随着拉应力的增大,抗压强度逐渐减少(拉压软化效应);当混土处于双向受压时,混凝土受压强度高于单轴抗压强度(强度增强效应),在双向等压时,约为16%。
也即在未对现行的混凝土的特性进行改变下fb0/fc0的取值为1+16%,即:
建议取值 fb0/fc0 =1.16
K(建议取值K=2/3)表征的是在最大主应力为负值,对于任意给定压力不变量p值的初始屈服处,拉伸子午线上的第二应力不变量q(tm)与压缩子午线上的q(cm)的比值,而且它必须满足0.5<K<1.0,如下图偏平面中的屈服面。
(3)粘性参数
混凝土损伤模型表现出软化行为和刚度退化的材料模型,经常在隐式分析程序中导致一些严重的收敛困难,例如在Abaqus/Standard中,由于刚度矩阵的集成奇异,导致计算不收敛。克服这些收敛困难的一种常用技术是使用本构方程的黏塑性来进行调整,对于足够小的时间增量,它可使软化材料的连贯切线刚度变成正值。
粘性系数取值偏大,结构有变刚的趋势;取值偏小,则分析运行越难于收敛。
粘性系数建议值为0.004(如果遇到收敛困难可将该数适当增大)
(注意:Abaqus/Explicit无收敛困难的问题,因此可默认粘性参数为0)
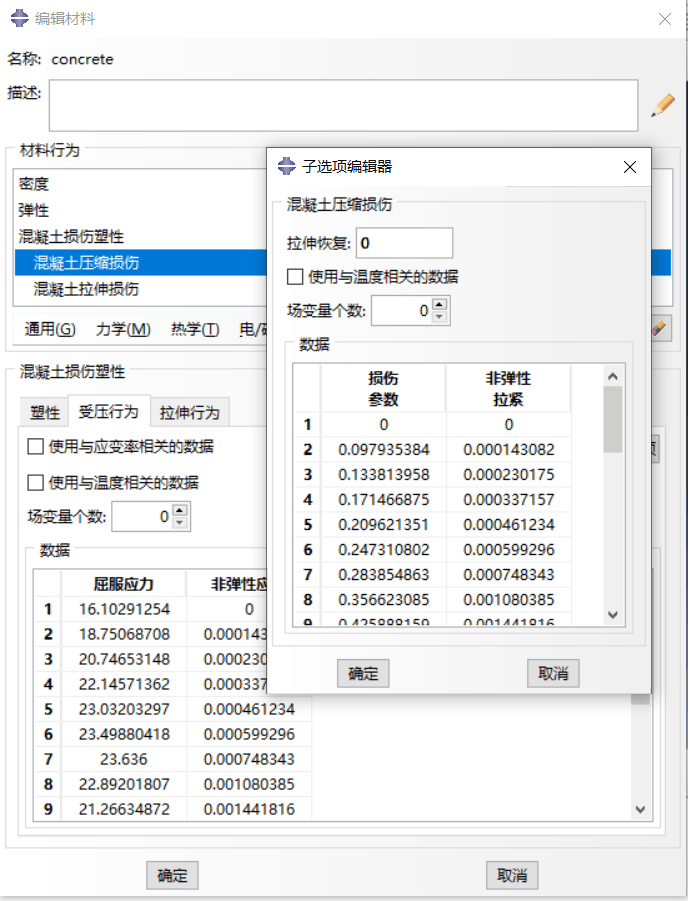
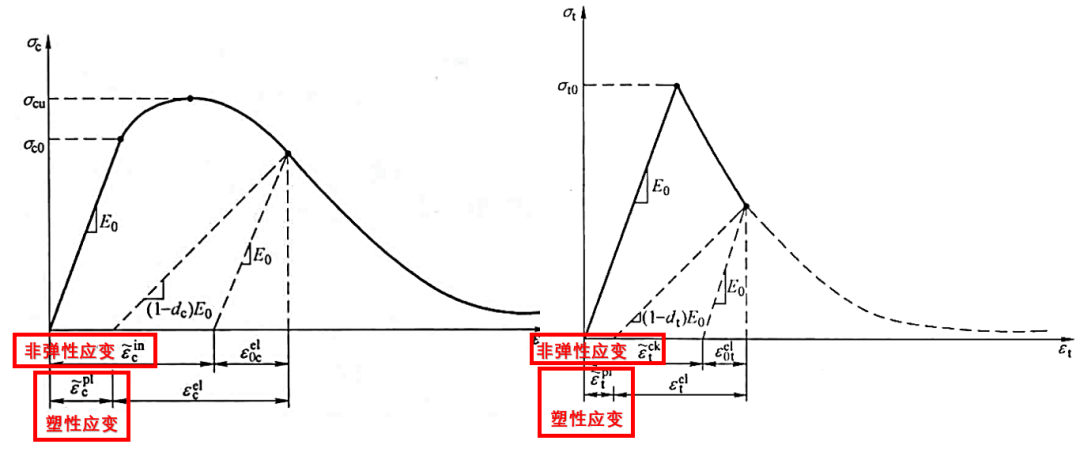
【受压受拉损伤定义】
如下图所示受拉受压行为的定义,在Abaqus-CDP中需要定义:受压行为(屈服应力、非弹性应变、压缩损伤参数、拉伸恢复)、受拉行为(屈服应力、非弹性应变、压缩复原)。
值得注意的是,在受拉行为中,通常应用可考虑拉伸的混凝土本构的应力-应变关系即可较好的模拟混凝土损伤。但同时Abaqus-CDP也提供了断裂能假设的方法来描述混凝土受拉行为,在本构填写受拉损伤dt的同时,则Abaqus自动采用下式将开裂位移值转换成“塑性位移”。因此从本质上讲,利用CDP在对混凝土构件做准静态或静态分析,建议使用应力-应变关系对混凝土的拉压行为进行描述。
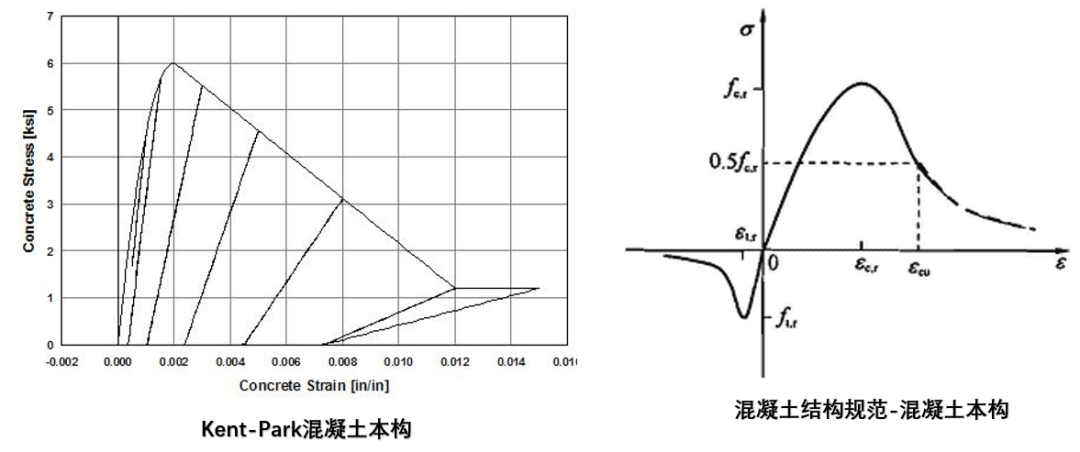
对于混凝土本构的定义,可采用Kent-Park混凝土本构、规范混凝土本构(常用)等混凝土本构对混凝土本构进行定义。
对于规范混凝土本构,特别需要注意的是对结构进行弹塑性分析时,规范中的 “损伤演化参数” Dc与 ABAQUS中的 “损伤因子” dc并不是一个概念,Dc为应力应变曲线上的割线损伤,而dc为卸载刚度损伤,因而在根据规范中的本构模型计算输入ABAQUS塑性损伤参数的时候,要进行相应的转换。
在弹性范围之外定义普通混凝土单轴压缩中的应力-应变行为。将压缩应力数据写成非弹性(或者压碎)应变的表格函数,如果需要也可以指定成应变率、温度和场变量的表格函数。应当为压缩应力和应变给出正的值(绝对值)。应力-应变曲线可以超出极限应力进行定义,进入应变软化区域。
应变数据以非弹性应变的形式给出,并以代替塑性应变出现。将压缩的非弹性应变定义成总应变减去响应未损伤材料的弹性应变。Abaqus使用下面的关系自动将非弹性应变值转换成塑性应变值:
特别注意:如果计算得到的塑性应变是负的并且/或者随着非弹性应变的增加而降低,则Abaqus发出一个错误信息,通常说明压缩损伤曲线是错误的。
对于实用性解决参数便携式计算问题,开发了关于Abaqus-CDP参数插件,如需要公众号后台回复:JYCDP 或 MACDP。详情可看:
关于拉伸恢复和压缩复原的问题对于该参数其导致的是会对于混凝土构件捏拢有一定的参考意义。
Abaqus对于混凝土损伤模型的刚度恢复直接提供了参数填写,拉伸恢复和压缩复原即为如下图所示即wt和wc的参数。绝大部分准脆性材料,包括对混凝土测试发现,当载荷从拉伸变化到压缩时,压缩刚度在裂纹闭合时恢复。另一方面,一旦产生了破碎微观裂纹,当载荷从压缩变化到拉伸的时候,拉伸刚度没有得到完全恢复。因此该参数对于混凝土捏拢具有一定的效果。
但特别要注意的是,并非任何钢筋混凝土构件都有捏拢现象,而捏拢现象的本质其实是钢材的塑性变形(主要)或者滑移而产生,而并非完全都是的滑移造成捏缩。
(下图给出了拉伸恢复和压缩复原从0到1的一个单轴荷载往复循环示意)
至此,已将Abaqus-CDP中的参数全部说明清楚,通过上述的理解,可以自行编写关于CDP本构的数据整理,也可通过下载相关插件进行安装使用。
完
更多精彩,关注建源学堂!
欢迎关注微信公众号: 建源学堂